Virtual areas in a matrix? If you consider a non-zero cell of a matrix to be a spot of an area, a larger such area constitutes by adjacent spots (non-zero cells). I consider them being rectangular when they cover an area of at least 2 x 2 cells of the matrix, better: at least 2 x 3 or 3 x 2. A 2 x 3 area equals the W network (3 x 2 is the M network; W and M networks both are kind N networks). Fine, so far. But virtual?
There might be lines of adjacent spots within the matrix, but the lines might be away from another line of spots, i.e. not adjacently. But some rows or columns away. These lines, together, although being disjacent, can get considered to constitute an area -- a virtual. That's because the x and y values represent a node each, hence the non-zero cells within the matrix are edges. There's really no need that the node which was set up to be column x to be fixed at that position. Hence, the columns -- and rows -- of the matrix are freely swappable. In other words, we shift around the marked spots within the matrix to get a real area.

See the picture aside: There are blue, red and green marked cells. Obviously, the blue spots form an area, since they neighbour each other.
The lower part of the green area is a step more complicated: We could get the 2 x 3 area, if we'd ignored the upper part of the green, by simply swapping columns 4 and 1. To get the remainder of the green, we need to swap rows 2 and 5. Which, of course would disrupt the blue area.
However, we could note down the blue area first and swap for the green area afterwards,
The red area, then, is the most complex one, at first glance, but after swapping around a bit, it gets found as well -- yet rather simply.
As the non-zero cells within the matrix are edges, a 10 x 10 matrix as a whole could contain up to a hundred different edges, i.e. get and be densely filled.
But there's a restriction with the matrix, not visible in the diagram: The columns and the rows represent the same nodes. So, as the MOM graph allows no loops, less than half of the matrix may be filled, actually, -- the upper right half of the matrix less the diagonal from top left to bottom right. So, in reality, the matrix never gets really dense.
However, I implemented the approach -- and while it worked fine with a matrix as small as 10 x 10 or 20 x 20, when I launched examination of a 1000 x 1000 matrix I quickly became aware, that approach might be "a bit" slow: It took hours on a 2 GHz machine (single core x86 CPU). Actually, the necessary processing time increased exponentially. -- And a thousand nodes is really not that much. Really, not even worth to mention: Just think about the number of words being part of a common day's news feed.
Well, now I developed another approach of detecting kind N networks within a MOM network, doing it by considering the edges only. That, effectively, leaves out the white spaces of the matrix.
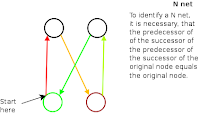
As before, I started with a relatively small net -- a hundred nodes and about 200 .. 250 edges. Which did it in less than half a minute, on a 400 MHz machine (single core CPU). Launching a 1000 nodes large test net with 2,500 to 5,000 edges, I learned it took about an hour. -- I became a bit scared because of that development, but then figured the reason for that slowness might be that it's just a 400 MHz machine only.
I put it onto the before mentioned 2000 MHz computer. -- The about 5000 edges got examined in less but three minutes. -- Phew!.
But I think, there are chances to speed up the approach, still. Anyone interested in improving the code or algorithm?
But, yes, sadly, I didn't check in the code yet, since I am after implementing detecting and replacing [the found] kind N networks. And the latter part I didn't figure out yet.
Updates: none so far

No comments:
Post a Comment